Residual connections使得网络变得更深,但作者从Ensembles角度来解释Residual Networks性能提升原因
Residual Networks Behave Like Ensembles of Relatively Shallow Networks从ensemble角度解释Deep Residual Networks。
深度残差网络,使网络的层数大大加深,网络的学习表达能力超过在此之前的所有网络。这篇文章从emsemble角度来解释其工作的原理,对比从残差角度来解释,似乎更有说服力。
残差网络与之前网络不同点
现代的计算机视觉系统架构都比较类似,都是输入low-level features,学习和和任务相关的high-level features。深度残差网络与之不同:1、引入了identity skip-connections,数据可以跳过某些层;2、skip-connections使得网络的深度多了两个量级,深度可达1202层;3、在测试阶段,移除某些层,对结果不会有显著影响,以往的网络结果,移除任何一层会对结果又非常大影响。
深度残差网络可以看过许多路径组成网络的一个集合。这些路径是否独立,它们之间是否有冗余?作者通过移除某些路径做实验,得出结论:深度残差网络是多个模型ensemble,逐渐移除路径,对结果的影响是平滑的。深度残差网络的路径不同,深度不同;路径的分布服从二项分布,意味着一个110层的网络实际大概深度只有55层。在训练过程中,梯度的来源更浅,只有10-34层。
残差网络展开后的形式
深度残差网络中,起作用的路径相对不深。深度残差网络并没有解决梯度消失的问题,它只是通过缩短有效连接路径使得网络变深。
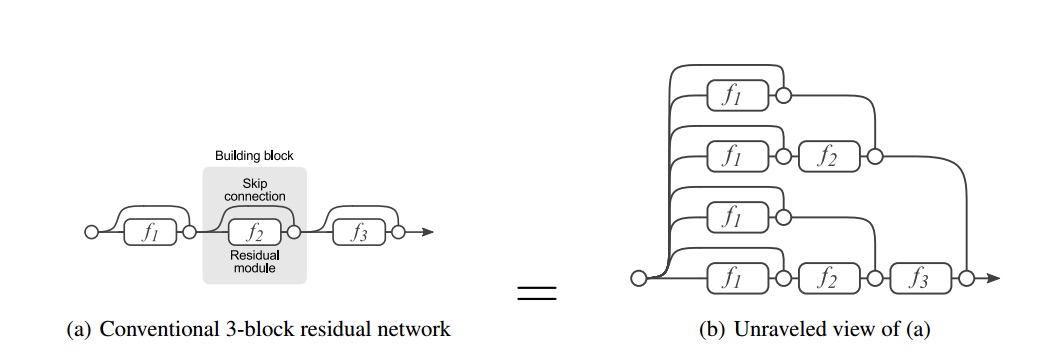
上图左边是一个残差网络结构,一个残差网络可以定义为:
$$
y_i = f_i(y_{i-1})+ y_{i-1}
$$
其中$f_i$是一个模块它中间可能经过了convoltion、batch normalization、ReLU。
右边是把左边网络展开后的结构,两者等同。从这个角度来看,残差网络显式连接路径有$O(2^n)$个。它的数学表示为:
\begin{align}
y_3 =& y_2 + f_3(y_2) \
=& [y_1 + f_2(y_1)] + f_3(y_1 + f_2(y_1)) \
=& [y_0 + f_1(y_0) + f_2(y_0 + f_1(y_0))] + f_3(y_0 + f_1(y_0) + f_2(y_0 + f_1(y_0)))
\end{align}
通过上面公式可以看出,数据有很多路径可以通过残差模块。对于一个残差模块,数据可以通过或跳过两种选择,对于$n$各残差模块,共有$2^n$条路径。
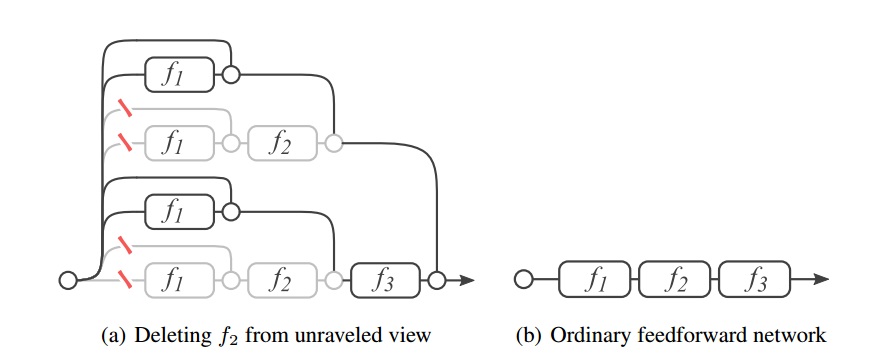
VGG和AlexNet这样序列网络结构(上图右边),网络数学表示为:
上图左边,残差网络除去$f_2$层,需要去掉4条路径。
实验
通过实验,在测试阶段,残差网络通过删除一些路径或残差模块,或者re-order残差模块,通过测试结果对比影响。。
路径对测试结果的影响
首先对比删除一个路径,即删除残差模块中的非线性部分,$yi = f(y{i-1}) + y_{i-1}$变为$yi = y{i-1}$。
1、在CIFAR-10数据集上,通过删除某些层,和VGG做对比: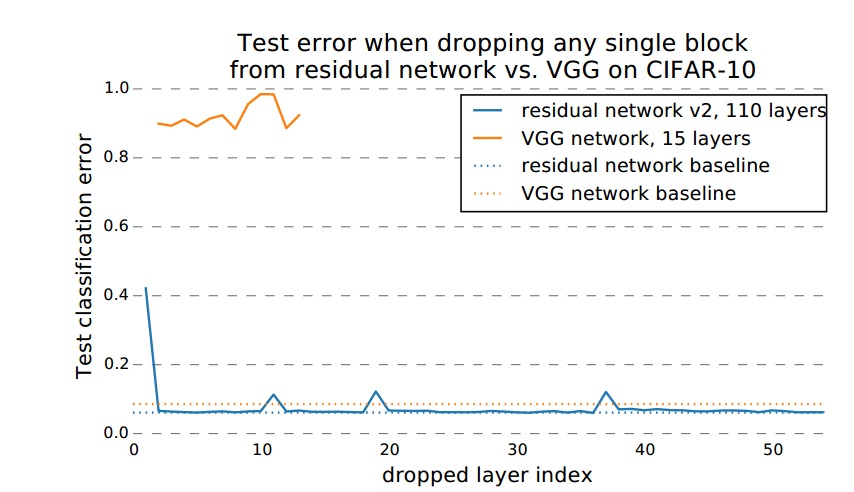
可以发现,VGG删除任何一层,测试结果相当于随机选择了。而残差网络不通,删除层对残差网络分类结果影响很小。
2、在ImageNet数据集上,训练200层网络,包含66个残差模块,删除第几个模块中的非线性部分对结果影响: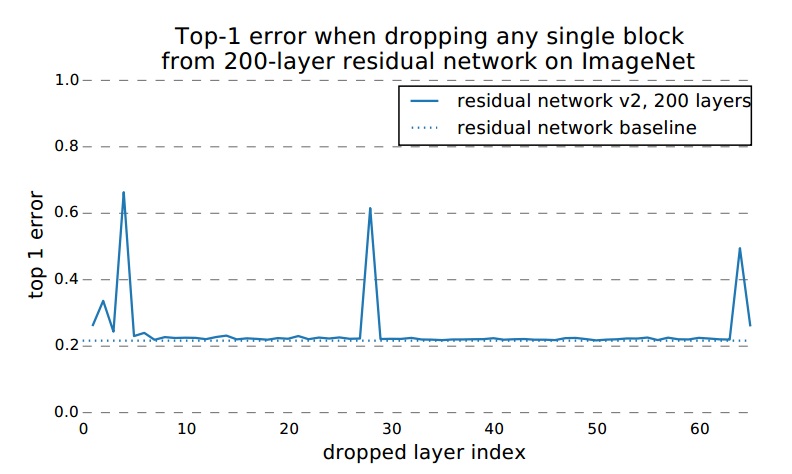
可以看出,残差网络中,路径虽然训练时在一起联合训练,但是它们之间并没有太强的依赖性。
模块对测试结果的影响
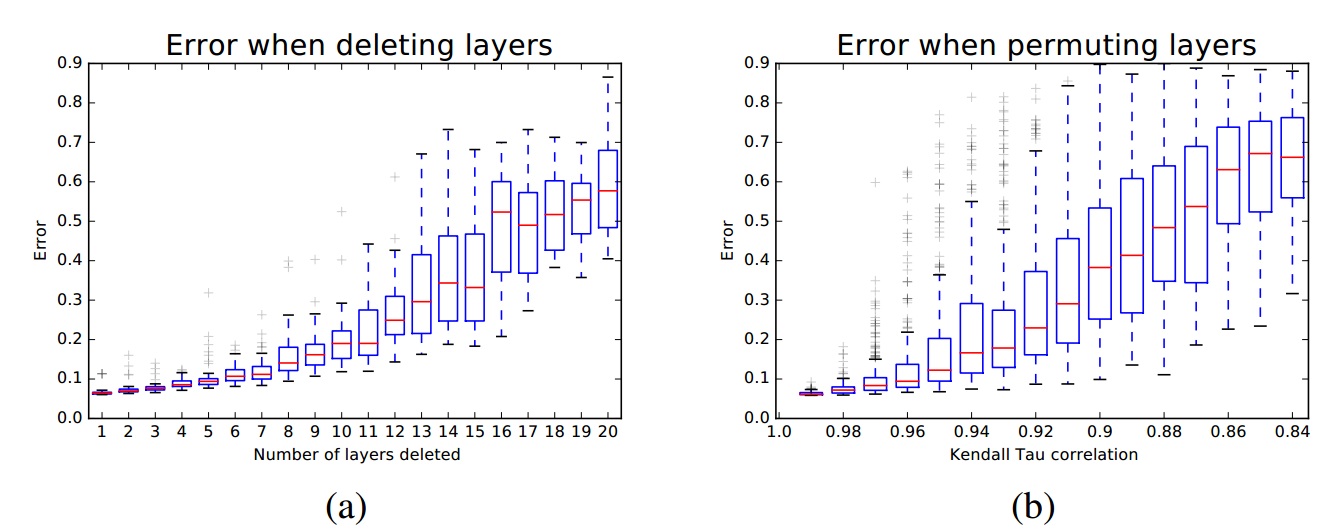
1、删除残差模块
删除$k$个残差模块,有效路径从$2^n$个变为$2{n-k}^$个。上面左图即为实验结果。随着删除模块增多,误差逐渐增大。这样的表现类似ensemble。
2、re-order模块
上面实验只是drop Layer,这里改变一下网络结构,re-order残差模块。这样相当于移除了某些模块,插入了新的模块。
re-order时,随机交换$k$对模块(模块之间匹配),使用Kendall Tau rank correlation coefficient可视化结果,如上图右边所示。
残差网络中的短路径非常重要
残差网络中的路径,并不是十分相互依赖,下面看一下它们的特点。
路径长度分布
包含$n$个残差模块的网络,只有1条路径是经过所有模块的,有$n$条路径只经过一个模块。路径分布服从二项分布;因此大部分路径长度为$n/2$,如上图(a)所示。例如一个包含54残差模块的网络,95%的路径只经过19到35个模块。
梯度消失
数据从各个路径传输,但是不同路径传递梯度不同。在反向传播时测量不同长度路径梯度大小。梯度幅度大小随路径长度变化如上图(b)所示,可以看出呈指数衰减。
有效路径相对较浅
通过测量不同长度路径对梯度贡献,找出有效路径。如上图(c)所示。一个54模块的残差网络,激活所有梯度贡献都来自第5-17模块,这些有效路径仅仅占所有路径额0.45%。
为了验证这一结果,对一个54模块的网络,训练它的子网络23个模块。最终对比得到,54模块的网络错误率为6.10%,23模块网络错误率为5.96%,两者之间没有显著差别。